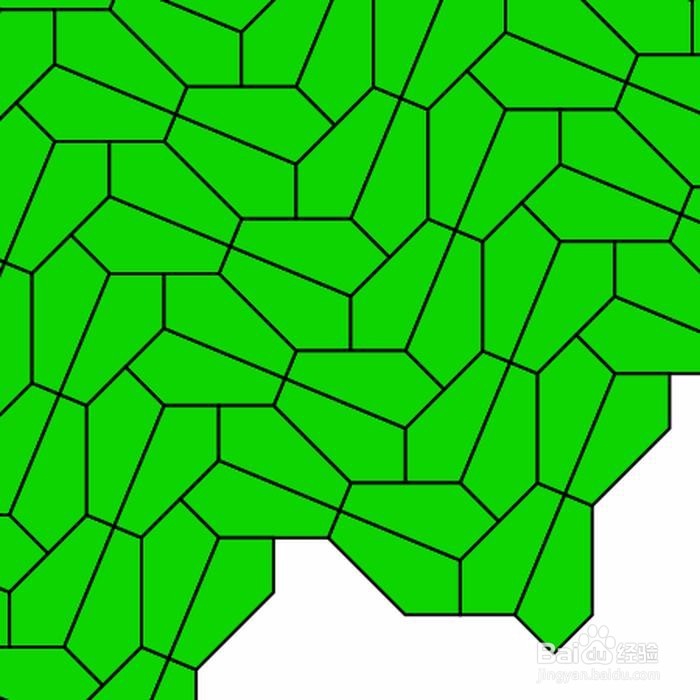
用全等的五边形铺砌平面问题的简单介绍

2024-11-02 11:10:42

五边形的铺砌问题，是寻找这样的五边形——用这种五边形的全等图形铺满整个平面，既不重合，又不留下空隙。五边形的铺砌问题，曾经在美国数学界和业余的数学爱好者之间引起空前的广泛讨论。现在各种高端的数学理论，却对这类简单的问题无计可施。要回答这类问题，智慧、机遇、勤奋缺一不可。即便如此，目前所发现的满足要求的五边形还不到20种，正是可遇而不可求。这里，我来把前人的发现简单地介绍一下。

工具/原料

几何绘图工具

电脑

问题的起源和历史

1、平面铺砌问题已经被很多数学家研究了近一百年，并取得了不少的成果，如：凸n边形（n≥7）不可能铺砌平面。具体的证明，请看下面这篇文章。

2、我们不考虑非凸的多边形，因为非凸多边形铺砌问题过于复杂，而且可行方案也很多。比如下图：凹十二边形铺砌平面。

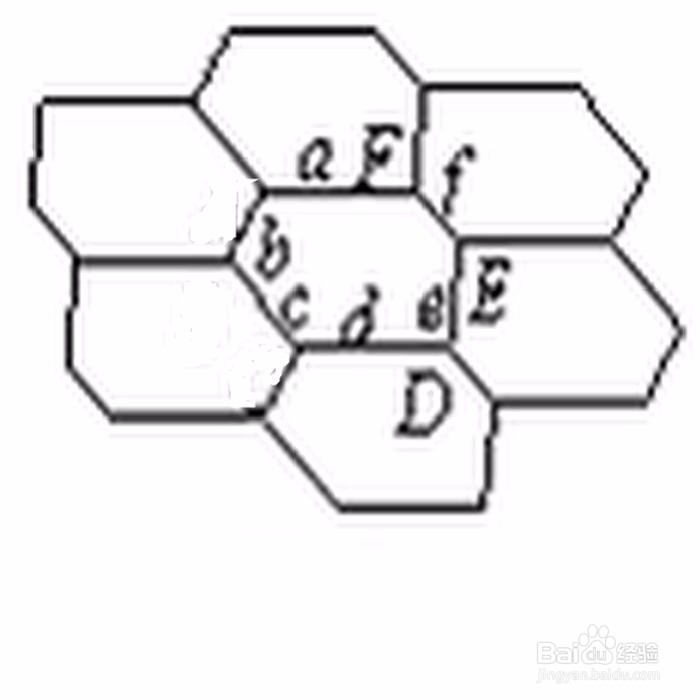
3、 1918年，数学家K·Reinhardt指出，能够铺砌平面的凸六边形共有三种。凸六边形ABCDEF，那么，能够铺砌平面的凸六边形需要满足：A+B+C=360° & FA=CD；A+B+D=360° & FA=CD & BC=DE；A=C=E=120° & AF=AB & BC=CD & DE=EF。下图是第一种情形：

4、 Reinhardt当年还给出了五种能够铺砌平面的凸五边形。 1968年，Kershner另外三种凸五边形。 1975年，美国数学家Martin Gardner在《科学美国人》的“数学游戏”专栏里写了一篇文章——《论用凸多边形铺砌平面》，把这八种凸五边形列举出来了。下面介绍一下这八种凸五边形。我们有必要认识一下马丁·加德纳！

马丁·加德纳列举的八种凸五边形

1、第一种情形：A+B+C=360°。

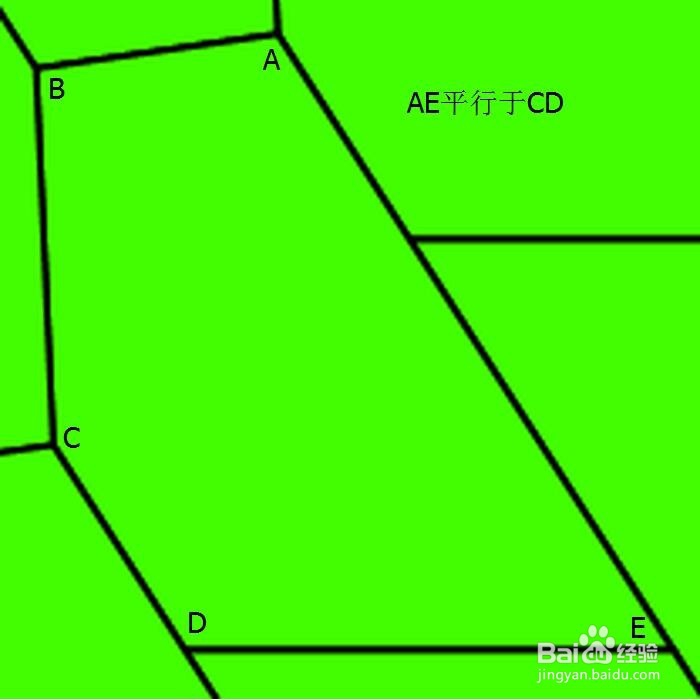
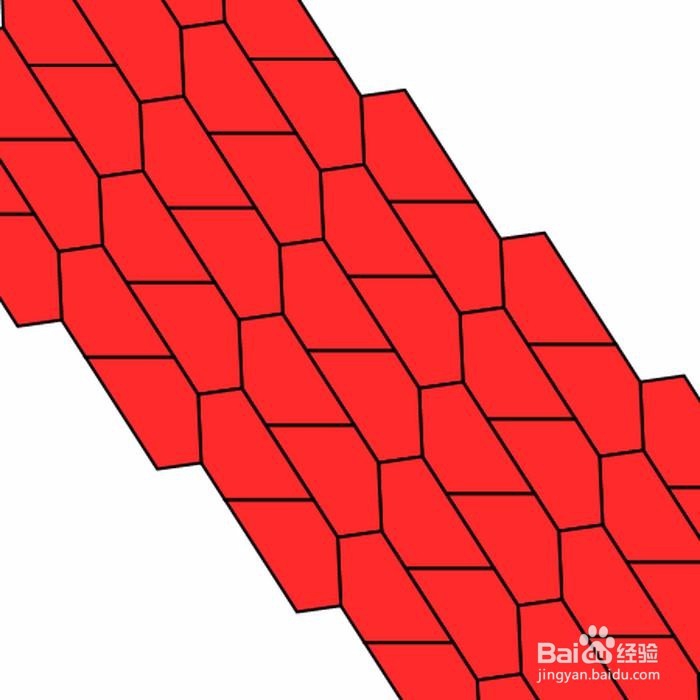
2、第二种情形：A+B+D=360° & AE=CD。

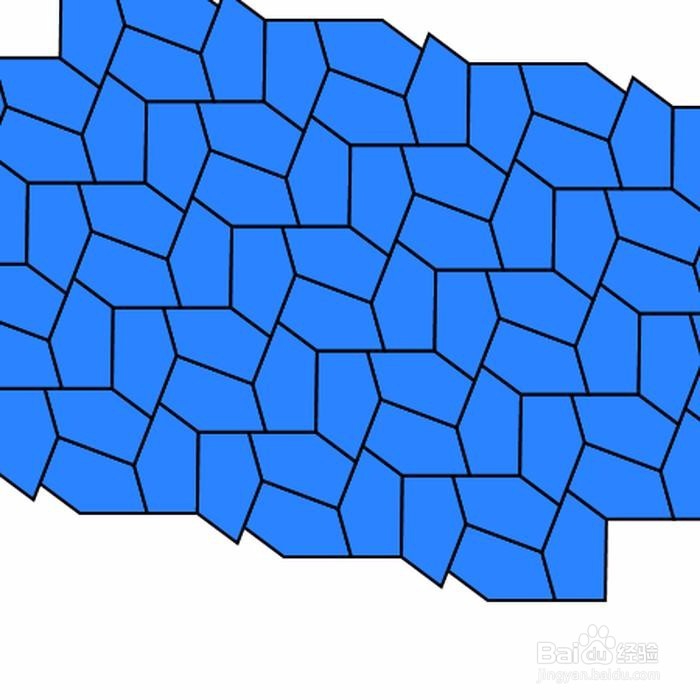
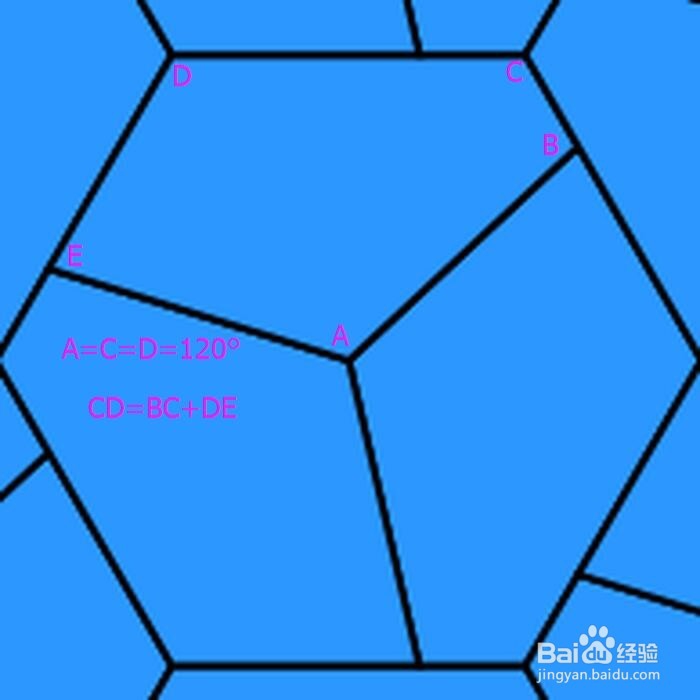
3、第三种情形：A=C=D=120° & AE=AB & CD=BC+DE。这样三个全等的凸五边形，恰好能够组成一个正六边形。

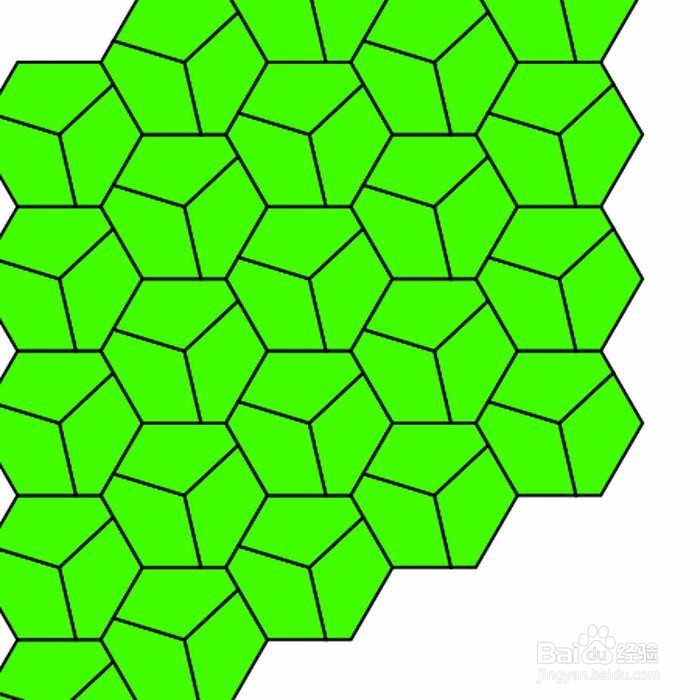
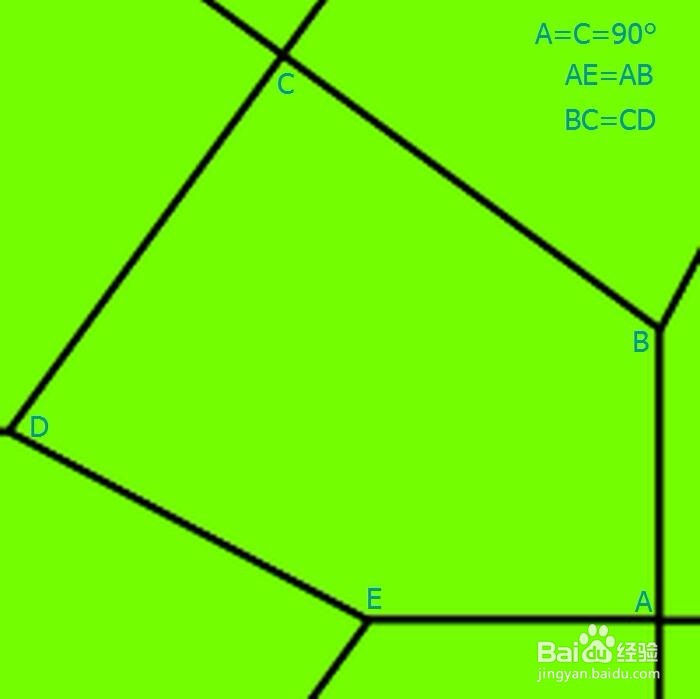
4、第四种，如：A=C=90° & AE=AB & BC=CD。

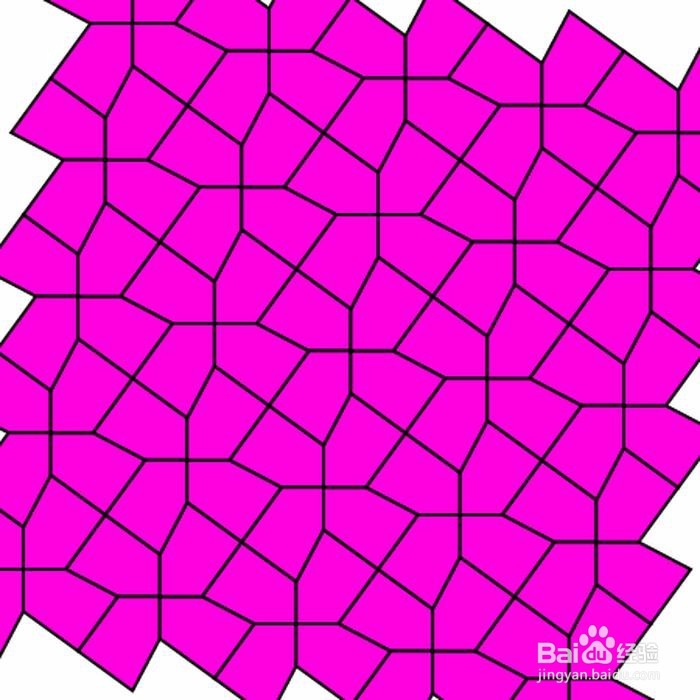
5、第五种情形的边、角度关系：A=60° & C=120° & AE=AB & BC=CD。

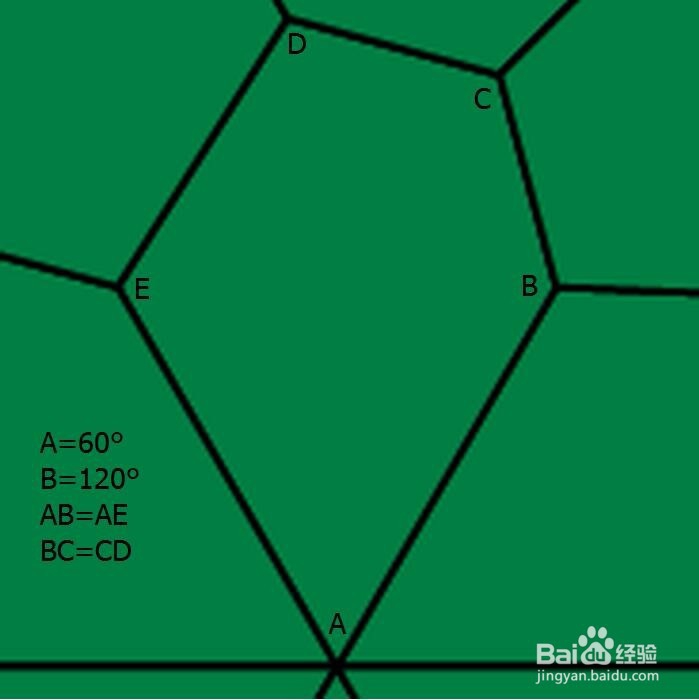
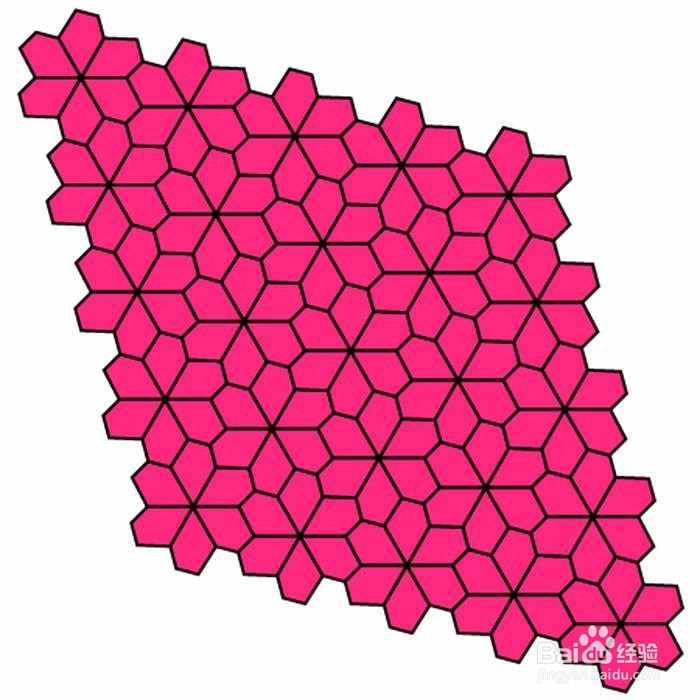
6、第六种是：A+B+D=360° & A=2C & AE=AB=DE & BC=CD。

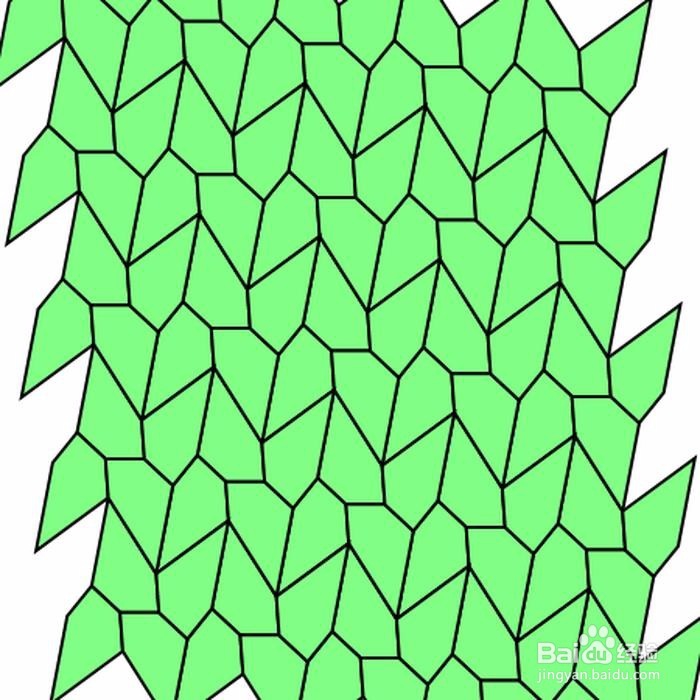
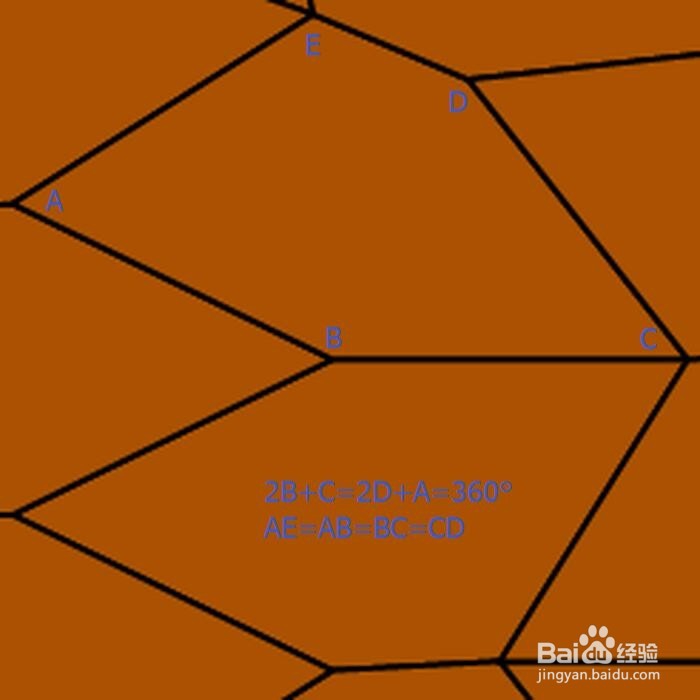
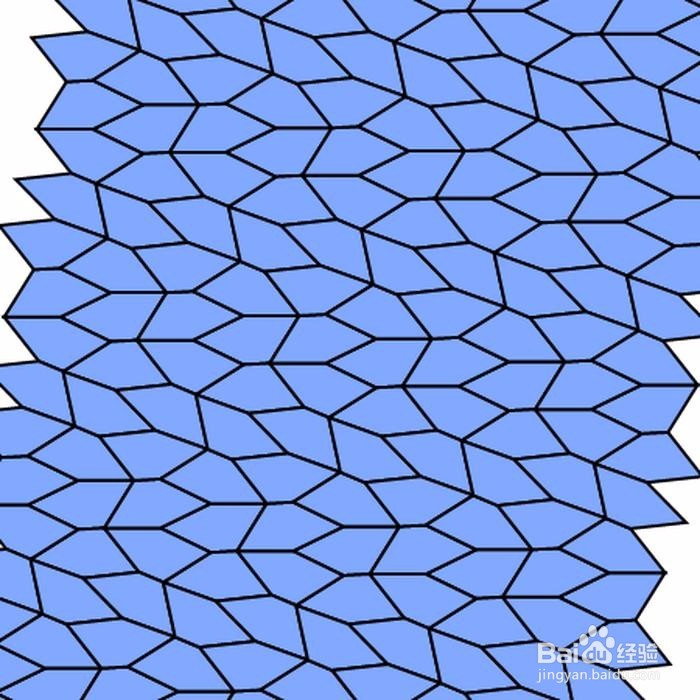
7、第七种情形的边和角的关系如下：2B+C=2D+A=360° & AE=AB=BC=CD。

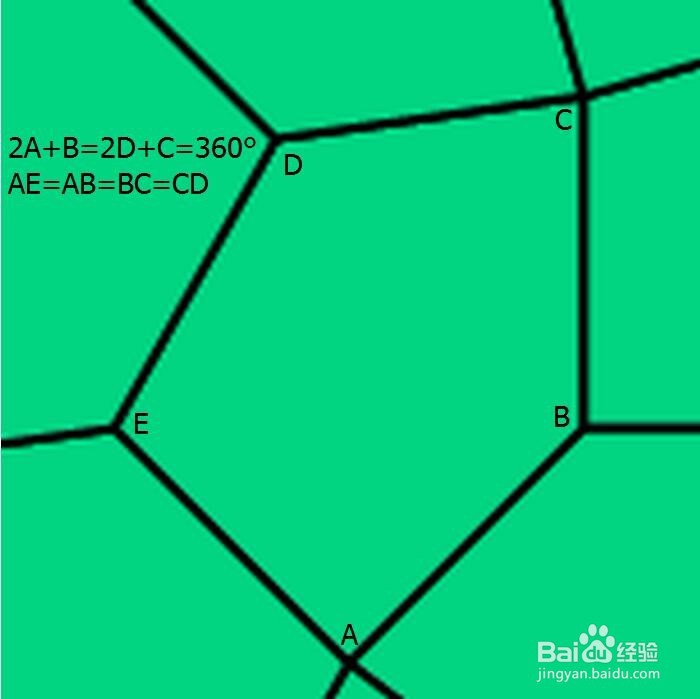
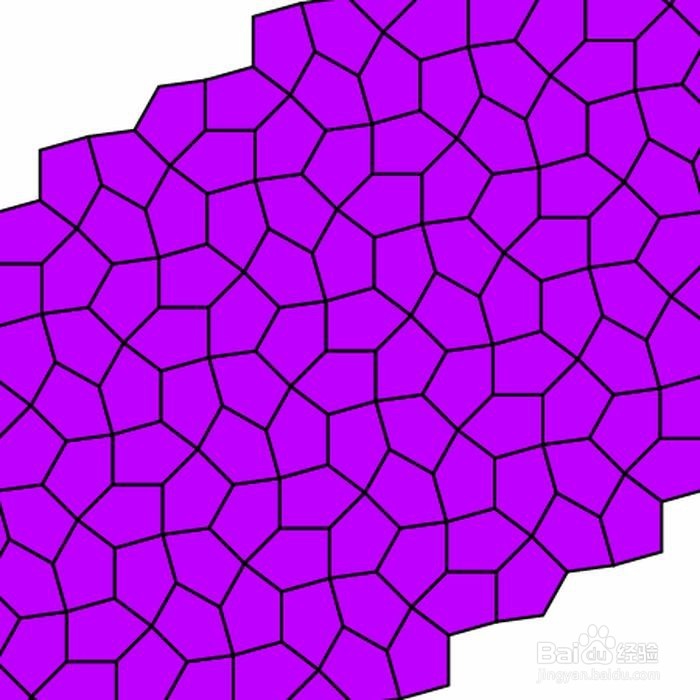
8、第八种情形如下：2A+B=2D+C=360° & AE=AB=BC=CD。 Kershner当时断言：能够铺砌平面的凸五边形，只有这八种。

Richard James的新发现

1、 Kershner的断言提出不久，计算机学家Richard James Ⅲ发现了一种新的凸五边形可以铺砌平面，其边和角满足：A=90°，B=102°，C=129°，D=141°，E=78°，AE+AB=BC+DE；或A=B=E=90°，C=D=135°，AE=AB=2BC=2DE。 1975年12月，马丁·加德纳把这一结果发表在《科学美国人》上。

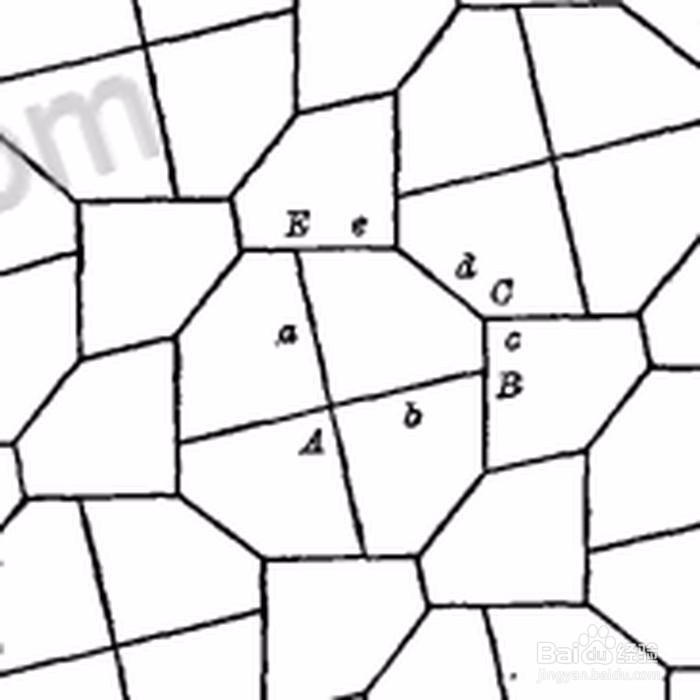
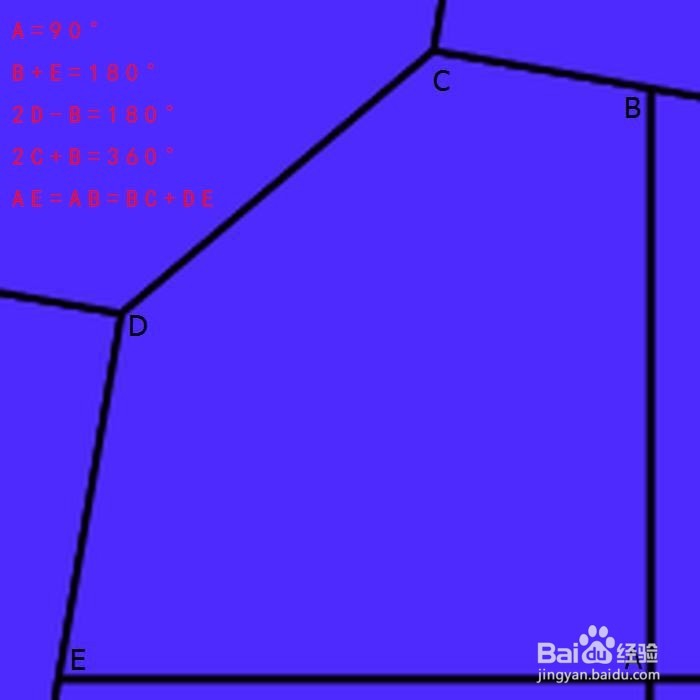
2、很快，数学家D·Schattschneider指出，Richard James发现的凸五边形应该归属于第九种（继前面提到的八种之后）：A=90°，B+E=180°，2D-B=180°，2C+B=360°，AE=AB=BC+DE。

Marjorie的成果展示

1、 Marjorie Rice在读她儿子订阅的杂志的时候，巧遇了马丁·加德纳的这篇文章，然后她就被深深地吸引住了——她说，去寻找新的五边形，那该是多么有趣的事情啊！当她专心致志地研究该问题的时候，竟然自创了一种专用符号（看下面的截图），使得观察图形的时候，方便了很多。

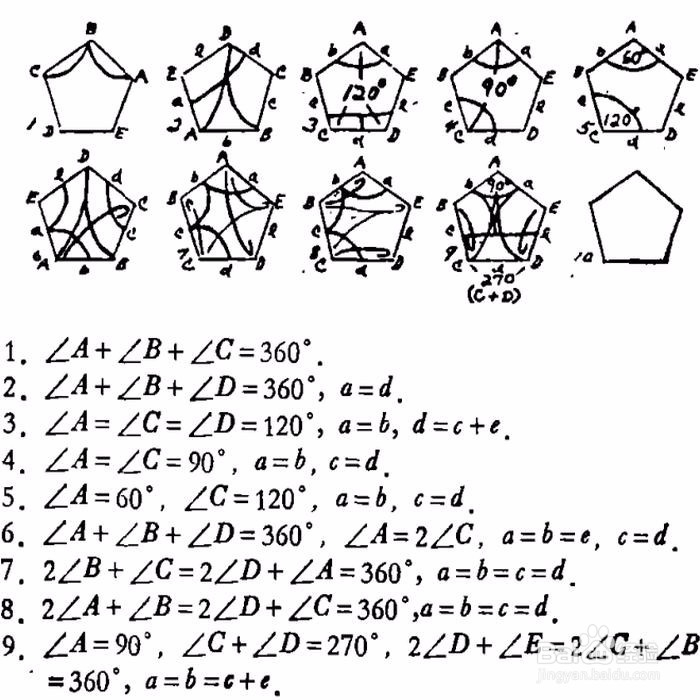
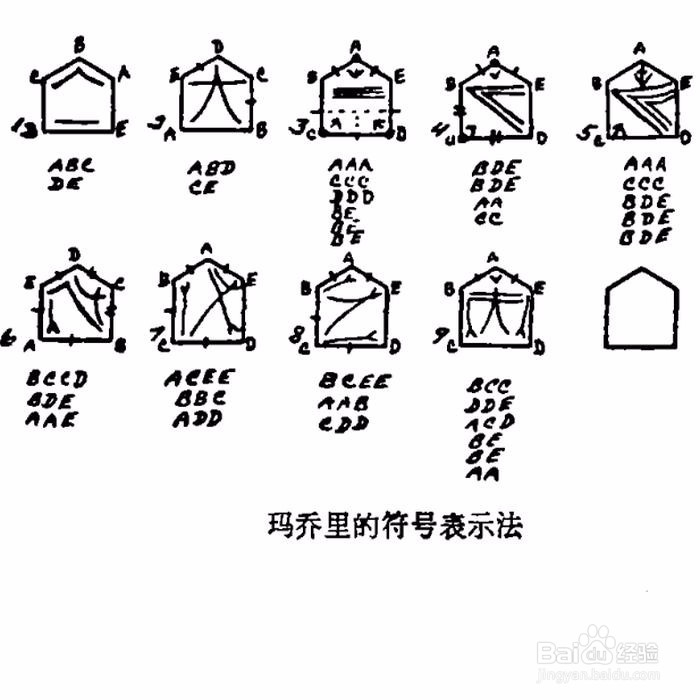
2、 1976年2月，Marjorie发现了一种新的五边形，它满足：2E+B=2D+C=360°，EA=AB=BC=CD。

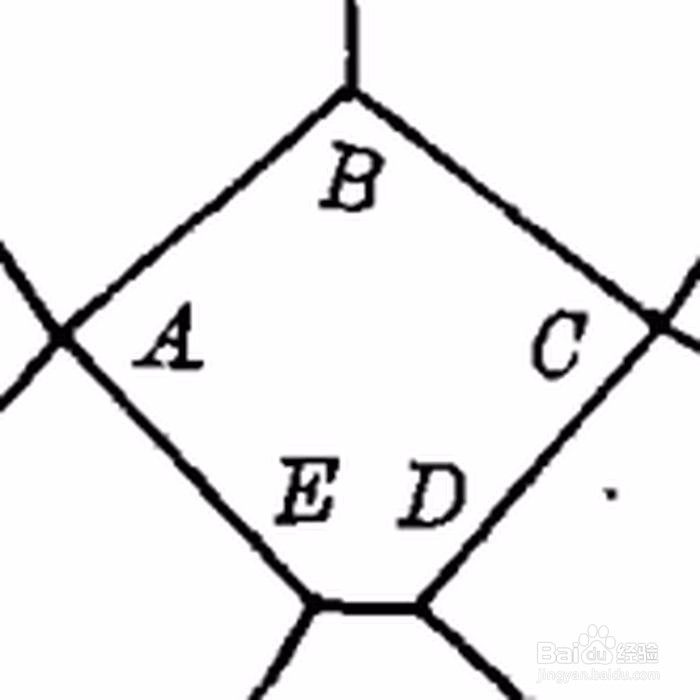
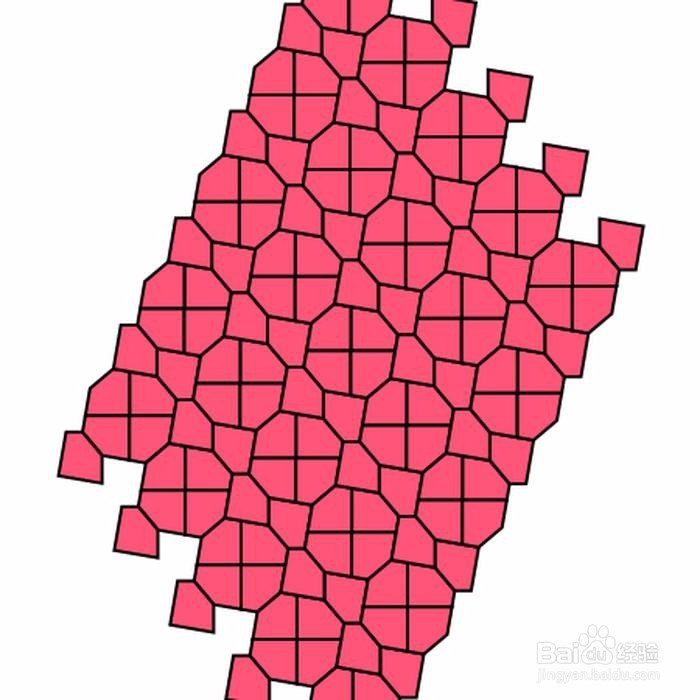
3、 Marjorie经过实践操作发现，同一种凸五边形可能有多种铺砌法。她在综合考察这前十种满足要求的凸五边形以后，找到了58种铺砌方法。下图，就是第一种凸五边形的另一种铺砌方法：

4、 1976年12月27日，Marjorie找到了两种新的凸五边形可以铺砌平面。其中一种是：D=90°，B+E=180°，2A+E=360°，2C+B=360°，AE=AB，2DE+BC=CD。

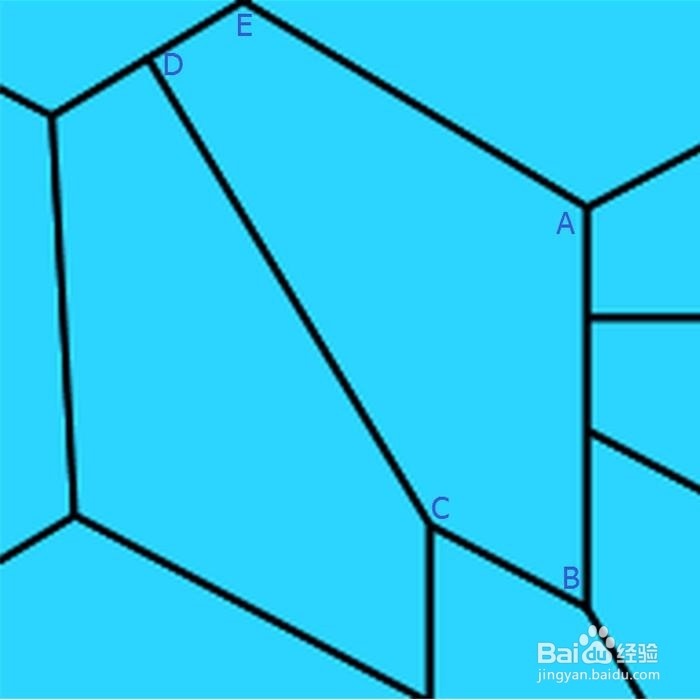
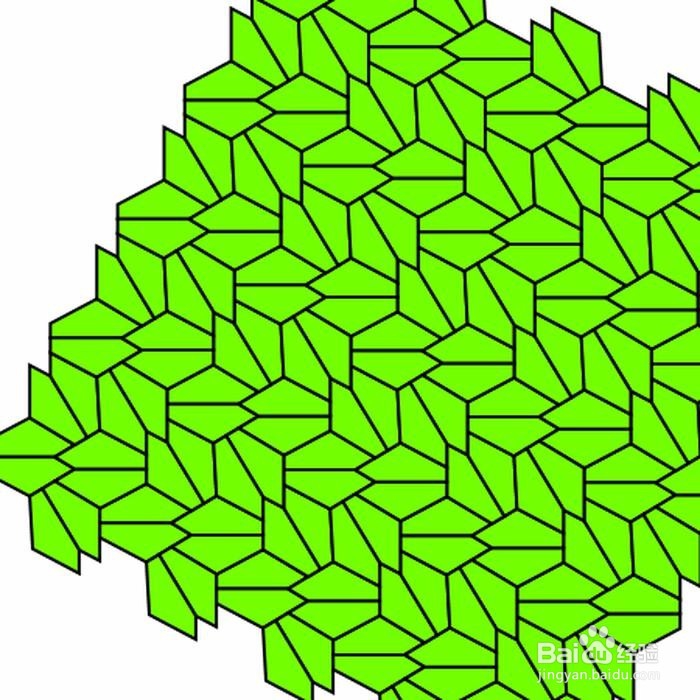
5、另一种新的凸五边形的边角关系是：D=90°，B+E=180°，2A+E=360°，2C+B=360°，AE+BC=AB，2DE=AB。这两种新的凸五边形，其实是把能够铺砌平面的“双六边形”裁切称为全等的四个凸五边形。

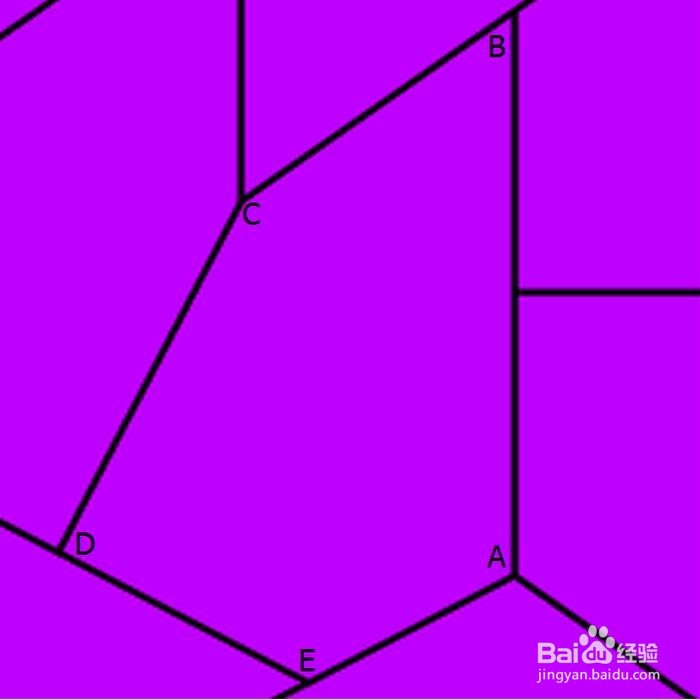
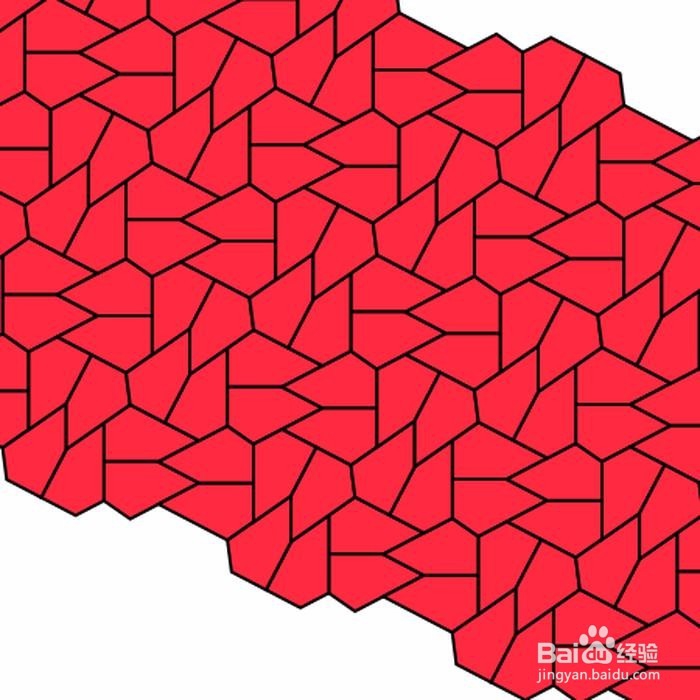
6、沉寂了近一年，Marjorie于1977年12月发现了第十三种，这次她裁切的是“双七边形”。边角关系如下：B=E=90°，2A+D=360°，2C+D=360°，2DE=2AE=CD。