【平面几何】凸四边形内部的一个作图问题
1、首先约定,AB和CD不平行,AD和BC不平行。否则需要另寻它法。

2、设AB和CD交于E,那么S(EAB)=S(ECD)=0。这是显然的。

3、点E沿着向量AB平移,得到点U;点E沿着向量DC平移,得到点V;构造平行四边形EUFV。
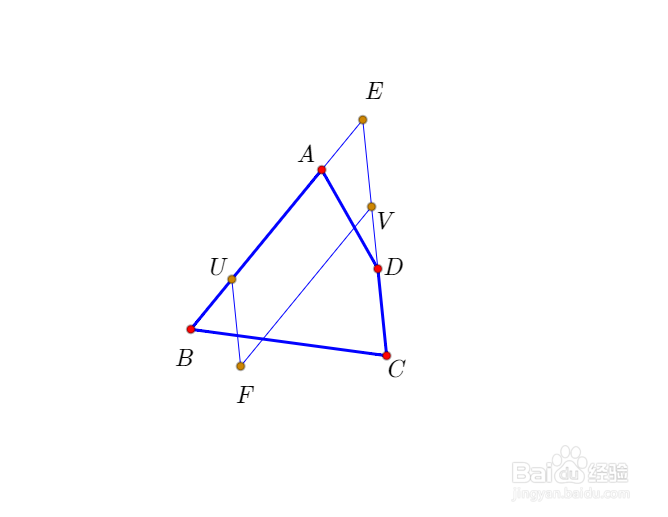
4、容易证明,对于直线EF上任意点X,都有如下结论:S(XEU)=S(XEV)=S(XAB)=S(XCD)

5、AD与BC交于点G,点G沿着向量DA平移至M,点G沿着向量CB平移至N,构造平行四边形GMHN,作直线GH。

6、直线EF和GH的交点,就是点O。这是唯一满足要求的点。

7、当AB与CD平行,AB和CD无法作出交点。这也是第一步的约定的根源。本文的方法,不是一个统一的方法,需要分类处理。那么,是否存在一个统一的方法,兼容平行与不平行的所有情形?
