法向量怎么求

1、曲线参数方程：{Sin[2 t], Cos[3 t], t/(Pi)}作图：ParametricPlot3D[{Sin[2 t], Cos[3 t], t/(Pi)}, {t, 0, 2 Pi}]

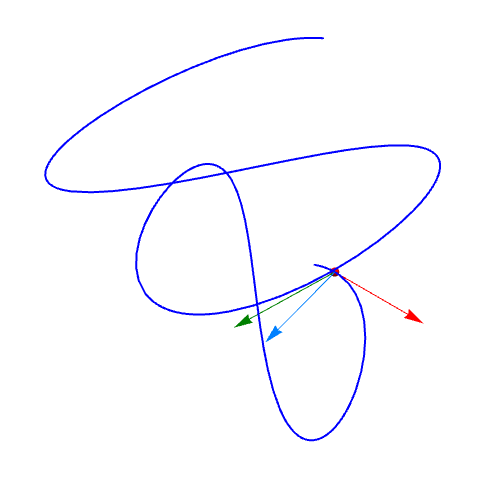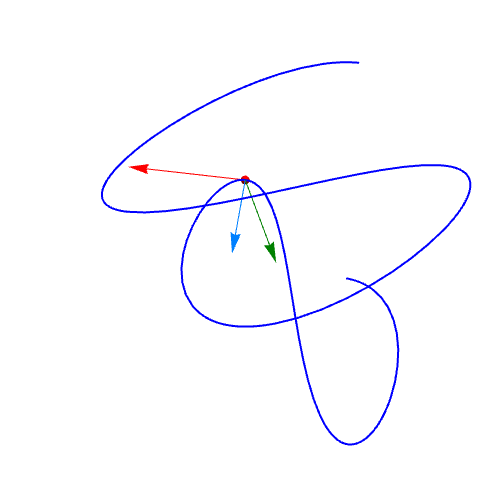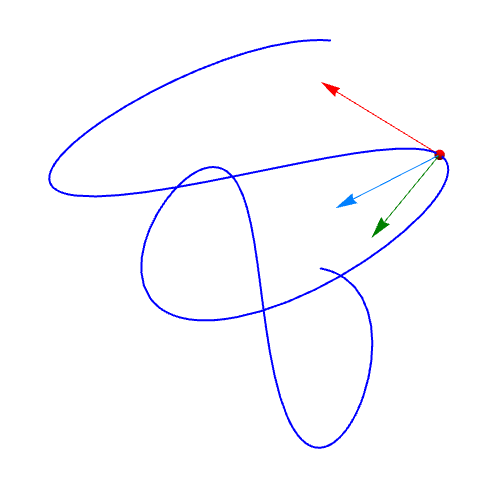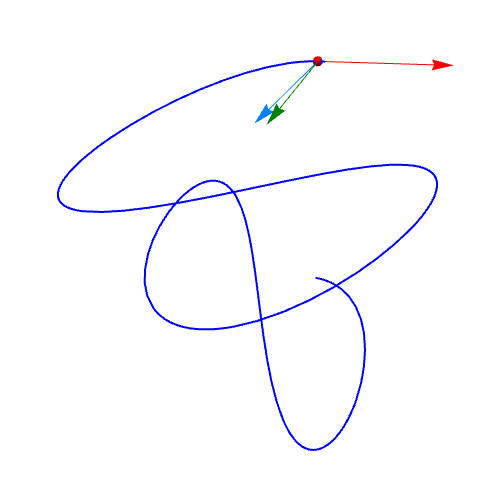
2、单位切向量的计算：qie = D[r, t]/Sqrt[D[r, t].D[r, t]] // FullSimplify绘制曲线上在t=1点处的单位切向量：Graphics3D[{Red, Arrow[{r, r + qie} /. t -> 1]}]

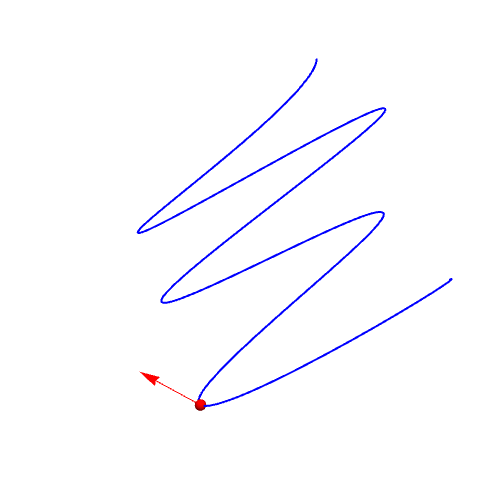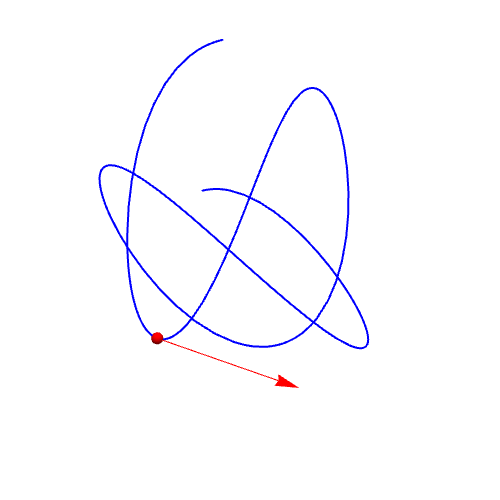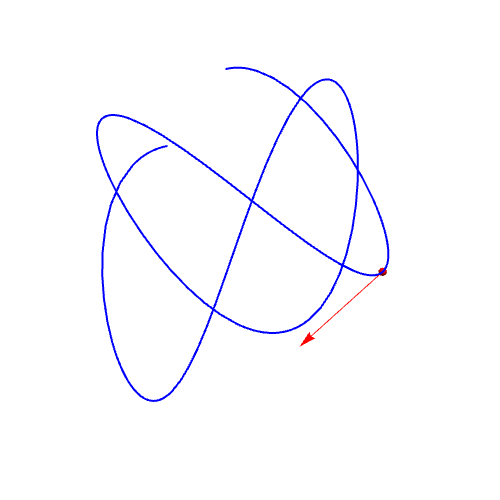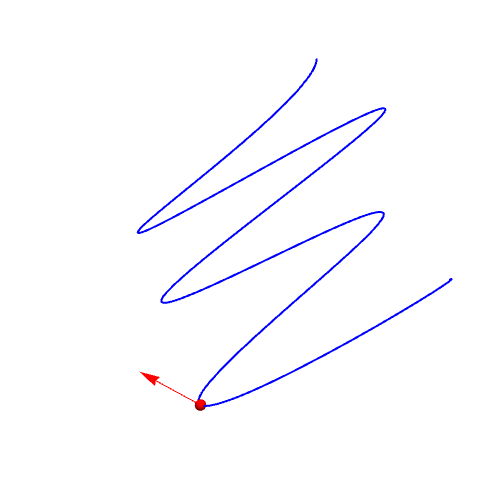
3、计算单位法向量：fa = D[qie, t]/Sqrt[D[qie, t].D[qie, t]];绘制单位法向量：Graphics3D[{RGBColor[0, 0.5, 0], Arrow[{r, r + fa} /. t -> 1]}]

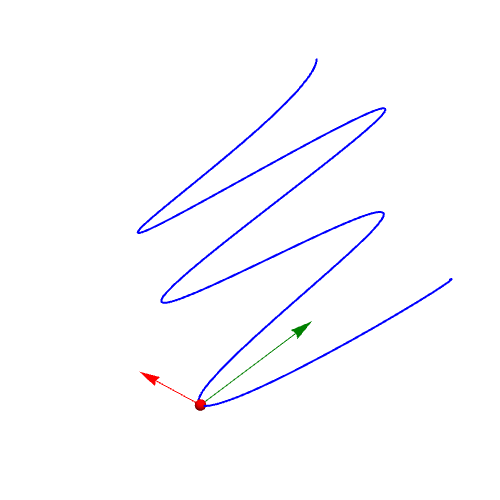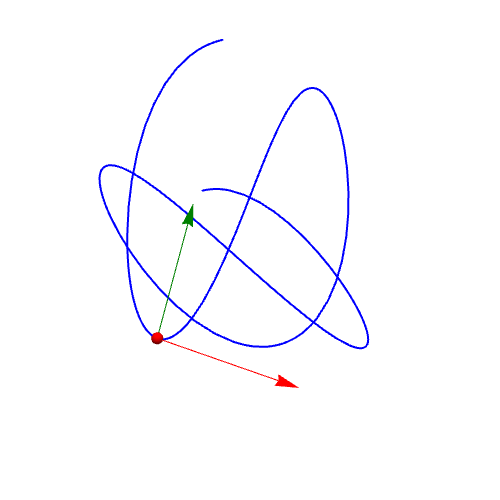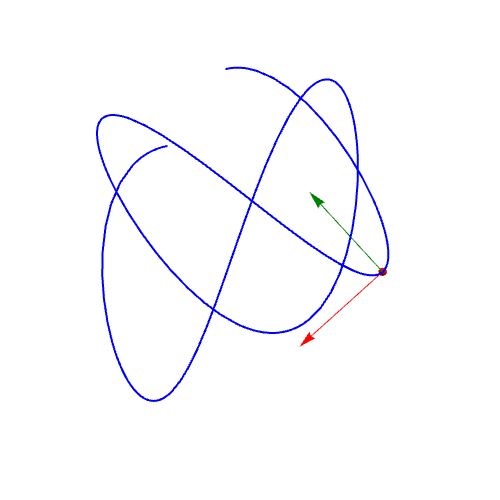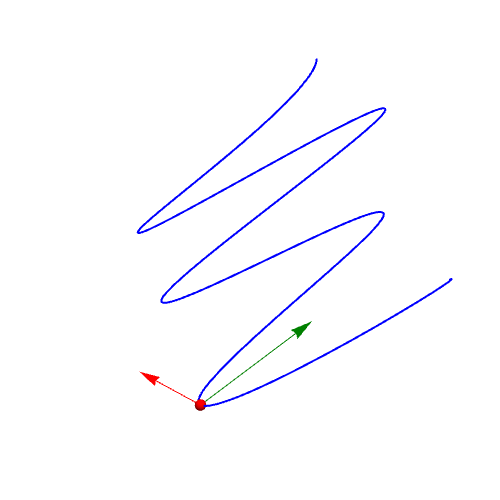
4、r关于t的二阶导数，一般情况下不是法向量：wei = D[r, {t, 2}]/Sqrt[D[r, {t, 2}].D[r, {t, 2}]]画图可知：Grap茑霁酌绡hics3D[{RGBColor[0, 0.5, 1], Arrow[{r, r + wei} /. t -> 1]}]可以发现，wei向量和fa向量不重合。

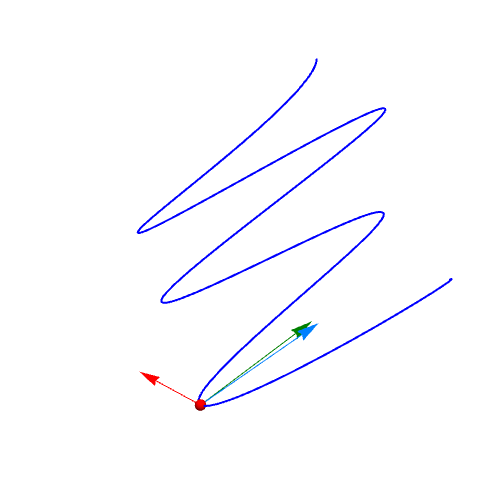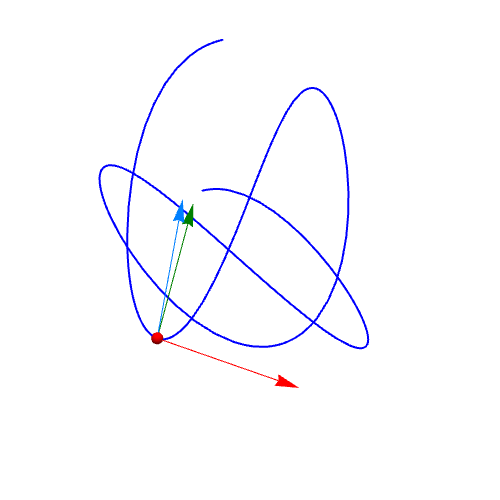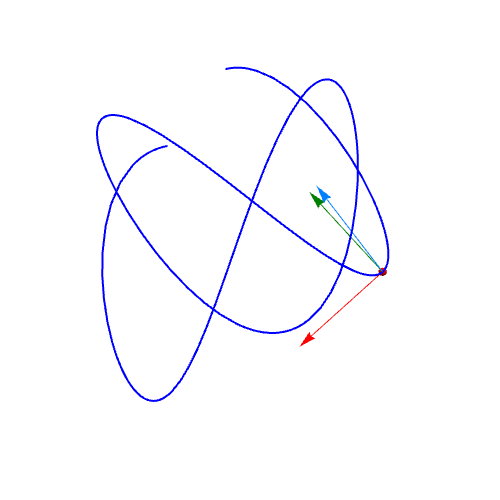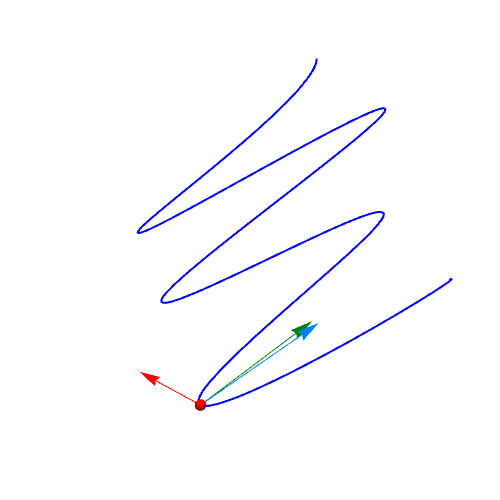
5、曲线上不同位置的法向量动态图。